
Often the complexity on one of Sharon’s projects is a combination of simple techniques, each of which can be isolated and easily mistressed*, which makes the whole experience satisfying on MANY levels!
Sharon’s new book, Crochet Scarves, Fabulous Fashions, Various Techniques is a perfect addition to her growing collection of “go-to” books for a crocheter of any skill level.
ANYONE can learn something from Crochet Scarves ending up with a lovely scarf in the bargain!
The thing about scarves is that they’re FUN to work up. I like to think of them as a huge swatch, and often use a scarf as an excuse to try a new stitch pattern or yarn. I also live in Minnesota and have two teenage children, so we can run through a LOT of scarves in a year.

- The finished product should be beautiful or visually compelling
- The techniques involved in the project must be interesting.
- I want to learn something from the creation of the project.
- The project must be FUN!

The scarves in this book fit all my criteria, with the added bonus that the charts are large and clear (and written in text, too) the technique images are plentiful and the patterns are well written.
One of my favorite projects is the simple mitered scarf which opens the book, Accordion Arrows.
This would be a HUGELY fun project to work up, one of those that would be as satisfying every step of the way, and garner as many compliments while it’s being worked as when it’s finished!
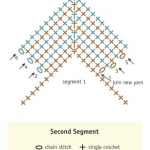
I really like how this pattern is explained in the book, and although the skill level is set at 3, I feel this would be an excellent project for a newer crocheter to move into a higher skill set – a project that would ‘grow’ a stitcher!

It would also be a GREAT project to use up stash! Imagine this worked in many different yarns, with one color used throughout as an accent to bring all the yarns together? THAT is a way to bust up that bag of yarns you’re hiding in the spare bedroom!
AND – here’s the good part – YOU can win a copy of this book!

Simply leave a comment telling me what your favorite crochet technique is. If you’re not a crocheter, make one up. If you’d like to link to a video or explanation of the technique, that would be great – that way we can ALL learn from your comment!
I’ll select one comment at random on Monday, July 30, and will notify the winner by email.
SO let’s hear what YOUR favorite crochet technique is – chop, chop!
*yes, I’m aware ‘mistressed’ not a real word, but I like to use it. Seriously, what is the percentage of women vs. men who are reading this right now?
I like to think in terms of ‘mistressing’ a technique, it’s one of my idiosyncrasies that make me so – what? – loveable? Irascible? Lovably irascible?


I don’t know if this counts but I started to use the Knook and I really like it. It allows me to crochet, which I know how to do, but make things that look knitted, which I am not very good at! Here is a video on how simple it is to pick up! Thanks for the chance to win!
http://www.youtube.com/watch?v=igAypsLsddI
Sure it counts! Thanks for the link!
And now, fun with emoticons…
🙂
🙁
😀
😮
😉
😐
I am definitely a baby crocheter… granny squares are my favorite because you can go as big or as small as you want, and they are great stash busters. I’d love a copy of the book… so I can “mistress” some more techniques! 🙂
Excited for a good new crochet book! Minnesota winters are great for them. 🙂 I’m not sure which my favorite crochet technique is at the moment, I’m kind of in a fun exploring time with some old crochet magazines I got from a friends mother. Amazing the details they put into it in the past!
Hi Annie. First of all I have been getting your newsletter since I first saw you on Knitty Gritty and made two tops from your beautiful patterns. So, today is the first time that I’ve read your blog. So, thank you. I like doing a single crochet when it looks like you’re making something very intricate. It’s such a simple stitch but can be made into something beautiful.
Cables! I am completely enamored with them! I haven’t been able to get my hands to function with knitting and I adore crochet so to be able to incorporate the beauty of cables into crochet makes me a very very happy woman =).
I haven’t done much with crochet in the last ???? years but I made granny square lapghans, different styles of hats and doilies when I was crocheting. My favorite was the doilies (I could see better than) made from the charts in Japanese books. I have been thinking about doing more crochet lately and scarves would be a great way to get back into it (minimal shaping and no concerns about gauge). Beth
Sorry to threadjack – just wanted to let you know I received the knitting needles and yarn today. Love the rowboats! And the yarn is nice and soft. Thank you again!
I’m glad to know it arrived! Isn’t that yarn delicious! It makes me sad that it’s not continued…
After being an avid knitter for 20+ years, I’ve been recently “hooked” (sorry) on crochet. Since I’ve literally only been crocheting for a month or so, my favorite technique is learning new techniques! As a lover of scarves, this book is for me–thanks for bringing it to my attention.
I’m just learning to crochet. I made a couple granny squares and a granny-style star this past week. I’m enjoying it, but pretty much all I know is chain, slip stitch, and double crochet, so it’s a little early to claim a favorite technique. I’d love to win this book – sounds like it has great projects to expand my so-far minimal crochet skills.
I learned to crochet many many moons ago but lately prefer to knit, but I really liked the pillow I made using the afghan stitch. Had to have each panel blocked and so totally clueless what this even was so sent if off to the dry cleaner to be blocked. I even did a cross stitch flower design on this pillow so I really ventured forth. Maybe I really like this stitch because it sure looks like stockinette doesn’t it?
I’m a crocheter from waaaaay back. Although I’ve been knitting more than I’ve been crocheting lately, crochet will always be my first love. My favorite crochet technique? Oh my. Tough question. I guess it would be crocheting around the front or back post. I love the dimension this gives to the work — so pretty! Hope I win the book, it looks fab!
I like top-down garments, broomstick lace, and tunisian/afghan crochet, but the method of join as you go motifs in Kristin Omdahl’s latest book blew my mind. Maybe I should have picked one of them for the Ravellenic Games, but I have too much else to finish! 🙂
I mostly knit but have been surprised at how much I’ve been enjoying crocheting small projects lately. Neckties and flowers. Also copying granny square pillow covers that my mom used to make. No particular favorite technique, but I really enjoy being able to make shapes with crochet, like the flowers. I was fascinated by forming a petal shape by using sc, hdc, and dc.
It took me a bit to understand the ‘mistressed’ – I like it!
I learned crochet from the babysitter when I was 10 or 12, and did granny squares, circles then strung through the center to make a doll, and zigzags, but not much else once I found knitting.
Recently, though, I have been learning the varieties of Tunisian crochet (my first attemtps were some personal variation!) and having some fun with that, when I can fit it into the knitting schedule!
Thanks for a chance at this book that looks quite interesting.
1. (quick answer) shell stitch & I love the rhythm of working on repetitive stitches.
2. Trying anything new …
3. Because I can’t knit anymore (major loss!), but can crochet (it doesn’t seem to aggravate my arms) Yea!
4. I have “Stash beyond belief” … looking for “Mr. Good Hook”.
If I don’t win this book, I will buy it so I can actually learn to crochet something other than using the single crochet ( love that one ) to edge knitted garments.
Well, I must confess to being a beginning crocheter. So far we have pot holders! And I’ve progressed from single crochet to half double to double! So, I don’t really have a favorite technique and haven’t done a lot with it. I think this book might help me develop some mad crochet skills!
I looove shells. I’m a girly-girl and they seem so feminine to me…plus they are fun to make
I love making crochet doilies and Tunisian crochet.
Picot stitch and corners (sort of the same!) Have afghan hooks and next on my list is Tunisian stitch
When I crochet I use a opening stitch marker to indicate if I’m crocheting right or left handed. Since I do both it keeps me from mixing them up mid project.
I’m a new crocheter, but I think the shell stitch is awesome. Not too hard to do, but it looks so fancy. Thanks for doing all the fun giveaways!
I am a crocheter who Loves tunisian, and scarves are so relaxing to do….hope I win this nice book!
My grandmother taught me how to make granny squares 50 years ago. Now I knit obsessively, but would try to pick up crocheting again with a neat book like this. Love, love, love that scarf!
Does this count?
i like to make baby blankets with different types of stitches. I am making granny stripes afghan right now like Lucy on Attic 24 made. I also like to make cables or lace baby afghans. Thank you for the opportunity to win this cool different book.
Would love this book; I am a beginning crocheter (since my mother failed to teach me and I learned after retiring). Can’t say which is my favorite technique, although I am very interesting in tapestry crochet.
Love to crochet and to knit. Enjoy combining the two and am also enjoying with different stitches in tunisian.
Granny Squares 4-evah! 🙂
I want that book! So I’m just going to have to buy it because I know you won’t pick me twice in a row to win. I’m still basking in the win of a new e-zine. yeah!! BTW, I guess my favorite crochet stitch is single crochet chain – because that’s all I know now to do!!! HA HA. Actually, I’ve seen pictures of “crocodile stitch” on Ravelry -and I am bugging my crochet friends to teach me how to do it. Looks really cool. Love you!
Hello – it’s me – token male reader of your blog. I don’t understand this word.
“*yes, I’m aware ‘mistressed’ not a real word, but I like to use it. Seriously, what is the percentage of women vs. men who are reading this right now? “
Mistressed, used in lieu of Mastered.